Question

Beth wants to plant a garden at the back of her house. She has 32m of fencing. The area that can be enclosed is modelled by the function A(x) = -2x2 + 32x, where x is the width of the garden in metres and A(x) is the area in square metres. What is the maximum area that can be enclosed?

Please help :(

Answer 1

The maximum area that can be obtained by the garden is 128 meters squared.

Explanation:

A represents area and we want to know the maximum.

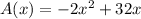`A(x)=-2x^2+32x` is a parabola. To find the maximum of a parabola, you need to find it's vertex. The y-coordinate of the vertex will give us the maximum area.

To do this we will need to first find the x-coordinate of our vertex.

to
`ax^2+bx+c` then
`a=-2,b=32,c=0[tex].</p><p></p><p>So the x-coordinate is [tex](-(32))/(2(-2))=(-32)/(-4)=8`.

To find the y that corresponds use the equation that relates y and x.

`y=-2x^2+32x`

`y=-2(8)^2+32(8)`

`y=-2(64)+32(8)`

`y=-128+256`

`y=128`

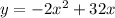
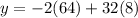
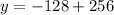
The maximum area that can be obtained by the garden is 128 meters squared.