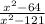Answer:
Problem:

Answer:
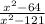
Explanation:

Writing as one fraction:

Now before we continue, notice both of your bottom and top are in the form of (a-b)(a+b) or (a+b)(a-b) which is the same format.
That is, we are multiplying conjugates on top and bottom.
When multiplying conjugates, all you have to do it first and last.
For example:
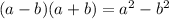 .
.
So your problem becomes this after the multiplication of conjugates: