Question

Which of the following recursive formulas represent the same arithmetic sequence as the explicit formula an=5+(n-1)2

a. a1=5
an=an-1+2
b. a1=5
an=(an-1+2)5
c. a1=2
an=an-1+5
d. a1=2
an=an-1*5

Answer 1

Answer: Option a

`\left \{ {{a_1=5} \atop {a_n=a_((n-1))+2}} \right.`

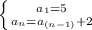
Explanation:

The arithmetic sequences have the following explicit formula

`a_n=a_1 +(n-1)*d`

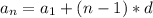
Where d is the common difference between the consecutive terms and
`a_1` is the first term of the sequence:

The recursive formula for an arithmetic sequence is as follows

`\left \{ {{a_1} \atop {a_n=a_((n-1))+d}} \right.`

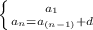
Where d is the common difference between the consecutive terms and
`a_1` is the first term of the sequence:

In this case we have the explicit formula
`a_n=5+(n-1)*2`

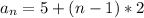
Notice that in this case

`a_1 = 5\\d = 2`

Then the recursive formula is:

`\left \{ {{a_1=5} \atop {a_n=a_((n-1))+2}} \right.`

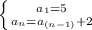
The answer is the option a.

Answer 2

Choice A:

`a_1=5`

`a_(n)=a_(n-1)+2`

Explanation:

`a_n=5+(n-1)2`

means we looking for first term 5 and the sequence is going up by 2.

In general,

`a_n=a_1+(n-1)d`

means you have first term
`a_1` and the sequence has a common difference of d.

So it is between the first two choices.

The explicit form of an arithmetic sequence is:
`a_n=a_1+(n-1)d`

An equivalent recursive form is
`a_n=a_(n-1)+d \text{ where } a_1 \text{ is the first term}`

So d again here is 2.

So choice a is correct.

`a_1=5`

`a_(n)=a_(n-1)+2`