Question

One x-intercept for a parabola is at the point

(2,0). Use the quadratic formula to find the
other x-intercept for the parabola defined by
this equation:
y = 4x2 - 4x – 8

Answer 1

(2,0) was already given so (-1,0) is the other one.

Explanation:

So we are asked to use the quadratic formula.

To find the x-intercepts (if they exist) is use:

`\text{ If } y=ax^2+bx+c \text{ then the } x-\text{intercepts are } ((-b \pm √(b^2-4ac))/(2a),0)`.

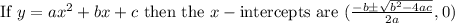Let's start:

Compare the following equations to determine the values for
`a,b, \text{ and }c`:

`y=ax^2+bx+c`

`y=4x^2-4x-8`

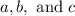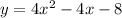
So

`a=4`

`b=-4`

`c=-8`

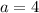
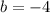
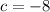
We are now ready to enter into our formula:

`x=(-b \pm √(b^2-4ac))/(2a)`

`x=(4 \pm √((-4)^2-4(4)(-8)))/(2(4))`

`x=(4 \pm √(16+16(8)))/(8)`

`x=(4 \pm √(16(1+8)))/(8)`

`x=(4 \pm √(16)√(1+8))/(8)`

`x=(4 \pm 4√(9))/(8)`

`x=( 4 \pm 4(3))/(8)`

`x=(4 \pm 12)/(8)`

`x=(4(1\pm 3))/(8)`

`x=(1(1\pm 3))/(2)`

`x=(1 \pm 3)/(2)`

`x=(1+3)/(2) \text{ or } (1-3)/(2)`

`x=(4)/(2) \text{ or } (-2)/(2)`

`x=2 \text{ or } -1`

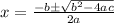
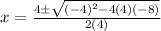
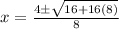
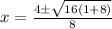
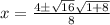
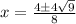
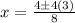
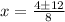
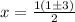
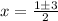
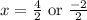
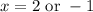
So the x-intercepts are (2,0) and (-1,0).

(2,0) was already given so (-1,0) is the other one.