Question

Madeline is standing 2x- 4 feet from the base of a tree. The height of the tree is 5x + 6 feet. Find the equation that shows

the straight-line distance from Madeline's feet to the top of the tree in terms of x.
Provide your answer below:

Answer 1

Madeline is standing 2x - 4 feet from the base of a tree, and the height of the tree is 5x + 6

Now we want to know the distance from Madeline's feet to the top of the tree.

You could picture it as a triangle rectangle, where the cathetus is the distance between Madeline and the tree and the distance between the floor and the top of the tree, in this case the distance between Madeline's feet and the top of the tree is the hypotenuse of such triangle rectangle, and can be obtained using the Pythagorean theorem: "the square of the hypotenuse is equal to the sum of the square cathetus"

then:

`H^2 = (2x - 4)^2 + (5x + 6)^2`

`H^2 = (4x^2 -16x + 16) + (25x^2  + 60x +36)`

`H^2 = (29x^2 + 44x + 52)`

`H = √( (29x^2 + 44x + 52))`

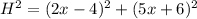
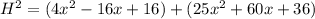
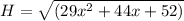
this is the distance from Madeline's feet to the top of the tree in terms of x.

Answer 2

c = sqrt( 29x^2 + 44x + 52)

Explanation:

This is an application of the Pythagorean theorem

c = sqrt(a^2 + b^2)

a = 2x - 4

b = 5x + 6

c = sqrt( (2x - 4)^2 + (5x + 6)^2 ) Substitute and expand

c = sqrt( 4x^2 - 16x + 16 + 25x^2 + 60x + 36) Collect like terms

c = sqrt( 4x^2 + 25x^2 - 16x + 60x + 16+36) Combine the like term pairs.

c = sqrt( 29x^2 + 44x + 52)

This does not factor into anything very nice.