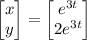In matrix form, the system is
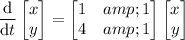
First find the eigenvalues of the coefficient matrix (call it
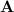 ).
).
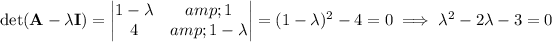
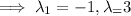
Find the corresponding eigenvector for each eigenvalue:
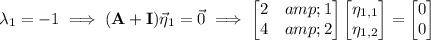
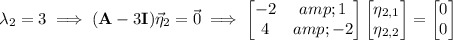
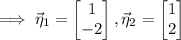
Then the system has general solution
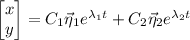
or
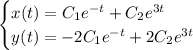
Given that
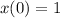 and
and
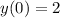 , we have
, we have
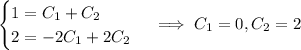
so that the system has particular solution