Answer:
The simplest form of the expression AB-C is
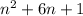 .
.
Explanation:
In this exercise we only need to use the properties of arithmetic operations and a minimal knowledge of algebraic notation. We have the expressions
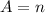 ,
,
 ,
,
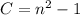 .
.
Now we make the indicated operations, beginning by AB:
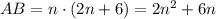 using the distributive property of multiplication.
using the distributive property of multiplication.
Then, we make AB-C:
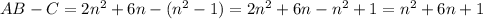 .
.
In the last step we must be vary careful with the change of signs in the expression inside parenthesis.