Question

X + y + w = b

2x + 3y + z + 5w = 6

z + w = 4

2y + 2z + aw = 1

For what values a, b (constants) is the system:

(a) inconsistent?

(b) consistent w/ a unique sol'n?

(c) consistent w/ infinitely-many sol'ns?

Answer 1

(a) a=6 and b≠
`(11)/(4)`

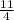
(b)a≠6

(c) a=6 and b=
`(11)/(4)`

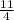
Explanation:

writing equation in agumented matrix form

`\begin{bmatrix}1 &1 & 0 &1 &b\\ 2 &3 & 1 &5 &6\\ 0& 0 & 1 &1 &4\\ 0& 2 & 2&a &1\end{bmatrix}`

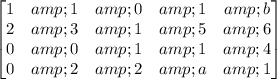
now
`R_(2) =R_(2)-2* R_(1)`

`\begin{bmatrix}1 &1& 0 &1 &b\\ 0 &1& 1 &3 &6-2b\\ 0& 0 & 1 &1 &4\\ 0& 2 & 2&a &1\end{bmatrix}`

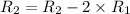
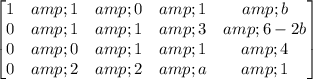
now
`R_(4) =R_(4)-2* R_(2)`

`\begin{bmatrix}1 &1& 0 &1 &b\\ 0 &1& 1 &3 &6-2b\\ 0& 0 & 1 &1 &4\\ 0& 0 & 0 &a-6 &4b-11\end{bmatrix}`

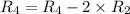
a) now for inconsistent

rank of augamented matrix ≠ rank of matrix

for that a=6 and b≠
`(11)/(4)`

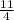
b) for consistent w/ a unique solution

rank of augamented matrix = rank of matrix

a≠6

c) consistent w/ infinitely-many sol'ns

rank of augamented matrix = rank of matrix < no. of variable

for that condition

a=6 and b=[tex]\frac{11}{4}

then rank become 3 which is less than variable which is 4.