Question

You are looking up at the top of a building at an angle of 30.6 degrees from the horizontal. If the building is 42.0m tall, how far are you from the building? Assume that you are 1.50m tall.

Answer 1

The distance between the person and the building is 68.48 meters.

Step-by-step explanation:

It is given that,

Angle of elevation, θ = 30.6 degrees

Height of building, MP = 42 m

Height of person, AB = 1.5 m

We need to find the distance between person and building. It is given by BP.

Since, MN + NP = 42

So, MN = 40.5 m

Using trigonometric equation as :

`tan\theta=(MN)/(AN)`

`tan(30.6)=(40.5)/(AN)`

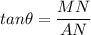
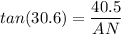
AN = 68.48 meters.

So, the distance between the person and the building is 68.48 meters. Hence, this is the required solution.