Question

Which of the formulas below could be a polynomial with all of the following properties: its only zeros are x = -6, -2, 2, it has y-intercept y = 4, and its long-run behavior is y rightarrow - infinity as x plusminus infinity? Select every formula that has all of these properties. A. y = -4/144 (x + 6)^2 (x + 2)(x - 2) B. y = -4/192 (x + 6)(x + 2)^4 (x - 2) C. y = -4x (x + 6)(x + 2)(x - 2) D. y = -4/24 (x + 6)(x + 2)(x - 2) E. y = -4/48 (x + 6) (x + 2)^2 (x - 2) F. y = -4/48 (x + 6)(x + 2)(x - 2)^2 G. y = 4/48 (x + 6)(x + 2) (x - 2)^2

Answer 1

A, B, and E

if I read your functions right.

Explanation:

It's zeros are x=-6,-2, and 2.

This means we want the factors (x+6) and (x+2) and (x-2) in the numerator.

It has a y-intercept of 4. This means we want to get 4 when we plug in 0 for x.

And it's long-run behavior is y approaches - infinity as x approaches either infinity. This means the degree will be even and the coefficient of the leading term needs to be negative.

So let's see which functions qualify:

A) The degree is 4 because when you do x^2*x*x you get x^4.

The leading coefficient is -4/144 which is negative.

We do have the factors (x+6), (x+2), and (x-2).

What do we get when plug in 0 for x:

`(-4)/(144)(0+6)^2(0+2)(0-2)`

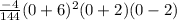
Put into calculator: 4

A works!

B) The degree is 6 because when you do x*x^4*x=x^6.

The leading coefficient is -4/192 which is negative.

We do have factors (x+6), (x+2), and (x-2).

What do we get when we plug in 0 for x:

`(-4)/(192)(0+6)(0+2)^4(x-2)`

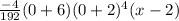
Put into calculator: 4

B works!

C) The degree is 4 because when you do x*x*x*x=x^4.

The leading coefficient is -4 which is negative.

Oops! It has a zero at 0 because of that factor of (x) between -4 and (x+6).

So C doesn't work.

D) The degree is 3 because x*x*x=x^3.

We needed an even degree.

D doesn't work.

E) The degree is 4 because x*x^2*x=x^4.

The leading coefficient is -4/48 which is negative.

It does have the factors (x+6), (x+2), and (x-2).

What do we get when we plug in 0 for x:

`(-4)/(48)(0+6)(0+2)^2(0-2)`

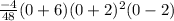
Put into calculator: 4

So E does work.

F) The degree is 4 because x*x*x^2=x^4.

The leading coefficient is -4/48.

It does have factors (x+6), (x+2), and (x-2).

What do we get when we plug in 0 for x:

`(-4)/(48)(0+6)(0+2)(0-2)^2`

Put into calculator: -4

So F doesn't work.

G. I'm not going to go any further. The leading coefficient is 4/48 and that is not negative.

So G doesn't work.

Answer 2

D.
`y=-(4)/(24) (x+6)(x+2)(x-2)`

Explanation:

Notice that we have 3 zeros, which means there are only 3 roots, which are -6, -2 and 2, this indicates that our expression must be cubic with the binomials (x+6), (x+2) and (x-2).

We this analysis, possible choices are C and D.

Now, according to the problem, it has y-intercept at y = 4, so let's evaluate each expression for x = 0.

C.

`y=-4x(x+6)(x+2)(x-2)\\y=-4(0)(0+6)(0+2)(0-2)\\y=0`

D.

`y=-(4)/(24) (x+6)(x+2)(x-2)\\y=-(4)/(24)(0+6)(0+2)(0-2)\\y=-(4)/(24)(-24)\\ y=4`

Therefore, choice D is the right expression because it has all given characteristics.