Question

Solve the system of equations.
y= 2x + 4
y = x2 + x - 2​

Answer 1

A.

Explanation:

`y=2x+4`

`y=x^2+x-2`

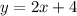
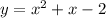
Both equations are solved for y so I'm just going to substitute

the 1st y (the 2x+4) into the second equation's y.

`2x+4=x^2+x-2`

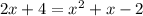
I'm going to get everything on one side so I have 0=ax^2+bx+c.

Subtract 2x and subtract 4 on both sides:

`0=x^2-x-6`

Since the coefficient of x^2 is 1, all we have to do is find two numbers that multiply to be -6 and add up to be -1.

These numbers are -3 and 2.

So the factored form of our equation is:

`0=(x-3)(x+2)`

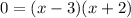
This means we have x-3=0 or x+2=0.

x-3=0

Add 3 on both sides:

x=3

x+2=0

Subtract 2 on both sides:

x=-2

So now we need to find y. I'm going to choose to use the easier equation:

y=2x+4.

If x=3, then y=2(3)+4=6+4=10. The ordered pair (3,10) is a solution.

If x=-2, then y=2(-2)+4=-4+4=0. The orded pair (-2,0) is a solution.