Answer:
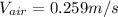
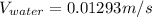
Step-by-step explanation:
Given data
Length of pipe
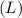 =13cm=0.13m
=13cm=0.13m
From tables at
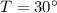
Kinematic viscosity of air
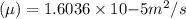
and reynolds number is given by
Re=
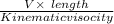
Flow is laminar up to Re.no. 2100
Re=
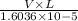
2100=
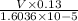
V=0.259 m/s
For water
Kinematic viscosity of water
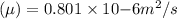
2100=
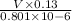
V=0.01293 m/s