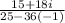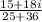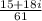Question

Simplify 3 divided by 5-6i

Answer 1

`(15)/(61)+(18)/(61)i`

Explanation:

`(3)/(5-6i)`

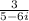
To simplify or to write in the form a+bi, you will need multiply the top and bottom by the bottom's conjugate like so:

`(3)/(5-6i) \cdot (5+6i)/(5+6i)`

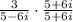
Keep in mind when multiplying conjugates you only have to multiply first and last.

That is the product of (a+b) and (a-b) is (a+b)(a-b)=a^2-b^2.

(a+b) and (a-b) are conjugates

Let's multiply now:

`(3)/(5-6i) \cdot (5+6i)/(5+6i)=(3(5+6i))/(25-36i^2)`

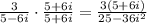
i^2=-1

`(15+18i)/(25-36(-1))`

`(15+18i)/(25+36)`

`(15+18i)/(61)`

`(15)/(61)+(18)/(61)i`

Answer 2

For this case we must simplify the following expression:

`\frac {3} {5-6i}`

We multiply by:

`\frac {5 + 6i} {5 + 6i}\\\frac {3} {5-6i} * \frac {5 + 6i} {5 + 6i} =\\\frac {3 (5 + 6i)} {(5-6i) (5 + 6i)} =\\\frac {3 (5 + 6i)} {5 * 5 + 5 * 6i-6i * 5- (6i) ^ 2} =\\\frac {3 (5 + 6i)} {25-36i ^ 2} =\\\frac {3 (5 + 6i)} {25-36 (-1)} =\\\frac {3 (5 + 6i)} {25 + 36} =\\\frac {3 (5 + 6i)} {61} =\\\frac {15 + 18i} {61}`

Answer:

`\frac {15 + 18i} {61}`