Question

I need help with this problem please.
​

Answer 1

b.

Explanation:

First off, let's name these endpoints. We will call them J(3, -2) and K(8, 0). The point we are looking for that divides this into a 3:1 ratio let's call L. We are looking for point L that divides segment JK into a 3:1 ratio.

A 3:1 ratio means that we need to divide JK into 3 + 1 equal parts, or 4. Point L divides JK into a 3:1 ratio. We need to find the constant of proportionality, k, that can be used in the formula to find the coordinates of L. k is found by putting the numerator of the 3/1 ratio over the sum of the numerator and denominator. Therefore, our k value is 3/4.

Now we need to find the slope of the given segment.

`m=(0-(-2))/(8-3)=(2)/(5)`

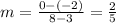
The coordinates of L can be found in this formula:

`L(x, y)=(x_(1)+k(run),x_(2)+k(rise))`

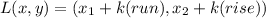
Filling in:

`L(x,y)=(3+(3)/(4)(5),-2+\frac{3}4}(2))`

Simplifying we have:

`L(x,y)=(3+(15)/(4),-2+(6)/(4))`

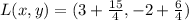
Simplifying further:

`L(x,y)=((12)/(4)+(15)/(4),(-8)/(4) +(6)/(4))`

And we have the coordinates of L to be

`L(x,y)=((27)/(4),-(1)/(2))`

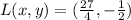
27/4 does divide to 6.75