Question

What hanging mass will stretch a 3.0-m-long, 0.32 mm - diameter steel wire by 1.3 mm ? The Young's modulus of steel is 20×10^10 N/m^2.

Answer 1

0.71 kg

Step-by-step explanation:

L = length of the steel wire = 3.0 m

d = diameter of steel wire = 0.32 mm = 0.32 x 10⁻³ m

Area of cross-section of the steel wire is given as

A = (0.25) πd²

A = (0.25) (3.14) (0.32 x 10⁻³)²

A = 8.04 x 10⁻⁸ m²

ΔL = change in length of the wire = 1.3 mm = 1.3 x 10⁻³ m

Y = Young's modulus of steel = 20 x 10¹⁰ Nm⁻²

m = mass hanging

F = weight of the mass hanging

Young's modulus of steel is given as

`Y = (FL)/(A\Delta L)`

`20* 10^(10) = (F(3))/((8.04* 10^(-8))(1.3* 10^(-3)))`

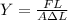
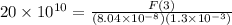
F = 6.968 N

Weight of the hanging mass is given as

F = mg

6.968 = m (9.8)

m = 0.71 kg