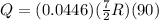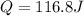Answer:
Q = 116.8 J
Step-by-step explanation:
Here given that the temperature of 1 L hydrogen is increased by 90 degree C at constant pressure condition.
So here we will have
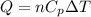
here we know that
n = number of moles
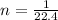
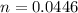
for ideal diatomic gas molar specific heat capacity at constant pressure is given as
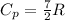
now we have