Question

Two cars are travelling with the same speed and the drivers hit the brakes at the same time. The deceleration of one car is a quarter that of the other. By what factor do the distances required for two cars to come to a stop differ?

Answer 1

The ratio of stopping distances is 4 i.e by a factor 4 the stopping distances differ

Step-by-step explanation:

Using 3rd equation of motion we have

For car 1

`v_(1)^{^(2)}=u_(1)^(2)+2a_(1)s_(1)`

For car 2
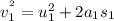
`v_(2)^{^(2)}=u_(2)^(2)+2a_(2)s_(2)`

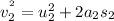
Since the initial speed of both the cars are equal and when the cars stop the final velocities of both the cars become zero thus the above equations reduce to

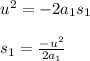`u^(2)=-2a_(1)s_(1)\\\\s_(1)=(-u^(2))/(2a_(1))`.............(i)

Similarly for car 2 we have

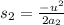`s_(2)=(-u^(2))/(2a_(2))`..................(ii)\

Taking ratio of i and ii we get

`(s_(1))/(s_(2))=(a_(2))/(a_(1))`

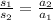
Let

`(a_(2))/(a_(1))=4`

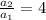
Thus

`(s_(1))/(s_(2))=4`

The ratio of stopping distances is 4