19 and 42 are coprime, so we can use the CRT right away. Start with
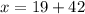
Taken mod 42, we're left with a remainder of 19. Notice that
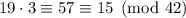
so we need to multiply the first term by 3 to get the remainder we want.

Next, taken mod 19, we're left with a remainder of 4. Notice that
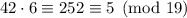
so we need to multiply the second term by 6.
Then by the CRT, we have

so that any solution of the form
 is a solution to this system.
is a solution to this system.