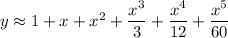We're looking for a solution of the form
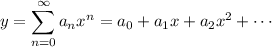
Given that
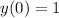 , we would end up with
, we would end up with
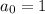 .
.
Its first derivative is

The shifting of the index here is useful in the next step. Substituting these series into the ODE gives
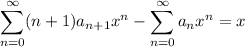
Both series start with the same-degree term
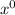 , so we can condense the left side into one series.
, so we can condense the left side into one series.
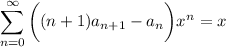
Pull out the first two terms (
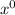 and
and
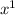 ) of the series:
) of the series:
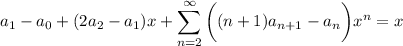
Matching the coefficients of the
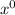 and
and
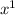 terms on either side tells us that
terms on either side tells us that
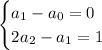
We know that
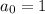 , so
, so
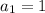 and
and
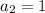 . The rest of the coefficients, for
. The rest of the coefficients, for
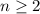 , are given according to the recurrence,
, are given according to the recurrence,
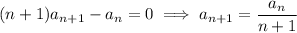
so that
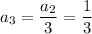 ,
,
 , and
, and
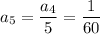 . So the 5th degree approximation to the solution to this ODE centered at
. So the 5th degree approximation to the solution to this ODE centered at
 is
is