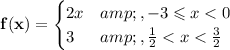Question

The graph represents the piecewise function

Answer 1

let's take a peek in the graph on the area from -3 to 0, namely -3 ⩽ x < 0, tis a line, so hmmm let's use two points off of it to get the equation hmmm (-3, -6) and (0,0)

`\bf (\stackrel{x_1}{-3}~,~\stackrel{y_1}{-6})\qquad (\stackrel{x_2}{0}~,~\stackrel{y_2}{0}) \\\\\\ slope = m\implies \cfrac{\stackrel{rise}{ y_2- y_1}}{\stackrel{run}{ x_2- x_1}}\implies \cfrac{0-(-6)}{0-(-3)}\implies \cfrac{0+6}{0+3}\implies \cfrac{6}{3}\implies 2 \\\\\\ \begin{array}ll \cline{1-1} \textit{point-slope form}\\ \cline{1-1} \\ y-y_1=m(x-x_1) \\\\ \cline{1-1} \end{array}\implies y-(-6)=2[x-(-3)] \\\\\\ y+6=2(x+3)\implies y+6=2x+6\implies y=2x`

now the smaller line from 1/2 to 3/2 well, heck is just a flat-line, namely y = 3

`\bf f(x)= \begin{cases} 2x&,-3\leqslant x < 0\\ 3&,(1)/(2)<x<(3)/(2) \end{cases}`