Question

travelling with velocity 1) Calculate the energy E (in eV) and direction vector Ω for a neutron v= 2132 +3300+154 k [m/sec]. (3 points) ^ ^

Answer 1

`K.E =0.081eV`

`\vec{\Omega}=(0.54\hat{i}+0.83\hat{j}+0.039\hat{k}`

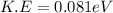
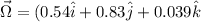
Step-by-step explanation:

Given:

Velocity vector
`\vec{v}=(2132\hat{i}+3300\hat{j}+154\hat{k})m/s`

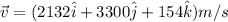
the mass of neutron, m = 1.67 × 10⁻²⁷ kg

Now,

the kinetic energy (K.E) is given as:

`K.E =(1)/(2)mv^2`

`\vec{v}^2 = \vec{v}.\vec{v}`

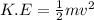
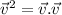
or

`\vec{v}^2 = (2132\hat{i}+3300\hat{j}+154\hat{k}).(2132\hat{i}+3300\hat{j}+154\hat{k})`

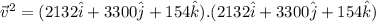
or

`\vec{v}^2 =15.45* 10^6 m^2/s^2`

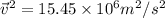
substituting the values in the K.E equation

`K.E =(1)/(2)1.67* 10^(-27)kg* 15.45* 10^6 m^2/s^2`

or

`K.E =1.2989* 10^(-20)J`

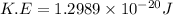
also

1J = 6.242 × 10¹⁸ eV

thus,

`K.E =1.2989* 10^(-20)* 6.242* 10^(18)`

`K.E =0.081eV`

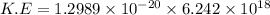
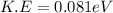
Now, the direction vector
`\vec{\Omega}`

`\vec{\Omega}=\frac{\vec{v}}{\left | \vec{v} \right |}`

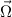
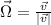
or

`\vec{\Omega}=\frac{(2132\hat{i}+3300\hat{j}+154\hat{k})}{\left |\sqrt{((2132\hat{i})^2+(3300\hat{j})^2+(154\hat{k}))^2} \right |}`

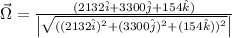
or

`\vec{\Omega}=\frac{(2132\hat{i}+3300\hat{j}+154\hat{k})}{3930.65}`

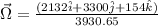
or

`\vec{\Omega}=0.54\hat{i}+0.83\hat{j}+0.039\hat{k}`