Question

Two resistors, the first 12 ? and the second 6 2, are connected in parallel to a 48 V battery What is the power dissipated by each resistor? A) P1 144 W, P2-288 W B) P1-162 W, P2-324 W C) P1-180 W, P2-360 W D) P1-192 W, P2 384 W

Answer 1

P₁ = 192 W and P₂ = 384 W

Step-by-step explanation:

It is given that,

Resistor 1,
`R_1=12\ \Omega`

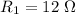
Resistor 2,
`R_1=6\ \Omega`

Voltage, V = 48 V

Power dissipated by resistor 1 is given by :

`P_1=(V^2)/(R_1)`

`P_1=((48)^2)/(12)`

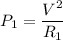
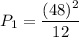
P₁ = 192 watts

Power dissipated by resistor 2 is given by :

`P_2=(V^2)/(R_1)`

`P_2=((48)^2)/(6)`

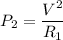
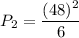
P₂ = 384 watts

So, the power dissipated by both the resistors is 192 watts and 384 watts respectively. Hence, this is the required solution.