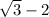Answer:
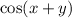 goes with
goes with

 goes with
goes with
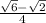
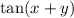 goes with
goes with
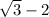
Explanation:
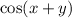
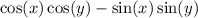 by the addition identity for cosine.
by the addition identity for cosine.
We are given:
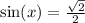 which if we look at the unit circle we should see
which if we look at the unit circle we should see
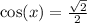 .
.
We are also given:
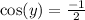 which if we look the unit circle we should see
which if we look the unit circle we should see
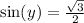 .
.
Apply both of these given to:
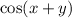
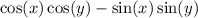 by the addition identity for cosine.
by the addition identity for cosine.

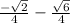
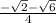

Apply both of the givens to:

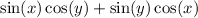 by addition identity for sine.
by addition identity for sine.
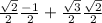
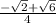
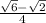
Now I'm going to apply what 2 things we got previously to:
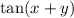
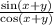 by quotient identity for tangent
by quotient identity for tangent
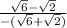
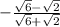
Multiply top and bottom by bottom's conjugate.
When you multiply conjugates you just have to multiply first and last.
That is if you have something like (a-b)(a+b) then this is equal to a^2-b^2.
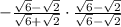
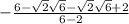
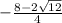
There is a perfect square in 12, 4.



Divide top and bottom by 4 to reduce fraction:
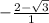

Distribute: