Question

The Sun radiates electromagnetic energy at the rate of 3.92 × 1026 W. The mass of the Sun is 1.99 × 1030 kg. What fraction of the Sun’s mass is lost during a human lifetime of 75 years? A. 2.16 × 10–13 B. 1.42 × 10–14 C. 6.90 × 10–14 D. 5.18 × 10–12 E. 8.63 × 10

Answer 1

D. 5.18 x 10⁻¹²

Step-by-step explanation:

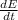`(dE)/(dt)` = rate at which sun radiates energy = 3.92 x 10²⁶ W

M = mass of sun = 1.99 x 10³⁰ kg

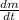`(dm)/(dt)` = rate at which sun's mass is lost

c = speed of light

Energy is given as

E = m c²

Taking derivative both side relative to "t"

`(dE)/(dt)=c^(2)(dm)/(dt)`

`3.92* 10^(26)=(3* 10^(8))^(2)(dm)/(dt)`

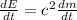
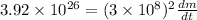
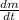`(dm)/(dt)` = 4.4 x 10⁹ kg/s

t = time interval = 75 yrs = 75 x 365 days = 75 x 365 x 24 hours = 75 x 365 x 24 x 3600 sec = 2.4 x 10⁹ sec

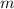`m` = mass lost

mass lost is given as

`m = t(dm)/(dt)`

`m = (2.4* 10^(9))(4.4* 10^(9))`

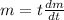
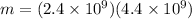
m = 10.56 x 10¹⁸ kg

fraction is given as

fraction =
`(m)/(M)`

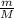
fraction =
`(10.56* 10^(18))/(1.99* 10^(30))`

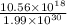
fraction = 5.18 x 10⁻¹²