Answer: a) k= 0.025
The exponential growth function in time t is given by :-
 ,
,
b) In year 2033 the population will reach to 176,000.
Explanation:
The exponential growth function in time t is given by :-
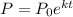 , where k is the rate of growth ,
, where k is the rate of growth ,
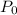 is the initial population.
is the initial population.
Given : In 2016 , the initial population of town =
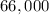
The rate of growth per year=

Which can be written as
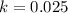
Let t be the number of years since 2016 to take population reach 176,000.
Then , the required equation will be :-
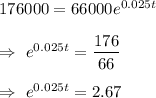
Taking log on both sides , we get
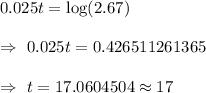
Thus it will take 17 years since 2016 to reach population 176,000.
Hence, In year 2033 the population will reach to 176,000.