Question

The perpendicular bisector of a chord XY cuts XY at N and the circle at P. Given that XY = 16 cm and NP 2 cm, calculate the radius of the circle.

Answer 1

17 cm

Explanation:

In the above figure the question has been explained

the perpendicular from circle on the chord divides chord into two halves

let r be radius of circle in triangle NOY

NO= PO-PN = r-2 and YO=r(radius) YN=8cm

applying pythagorus theorem

`r^(2) =8^(2) +(r-2)^(2)`

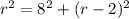
after rearranging and solving the equation we get

r=17 cm

therefore the radius of the triangle is 17 cm

note: on observing we find that the sides of triangle are pythagorian triplet 17, 15 and 8