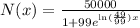Answer:
Explanation:
The logistic equation is
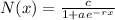
where:
c/(1+a) is the initial value.
c is the limiting value
r is constant determined by growth rate
So we are given that:
N(0)=500 or that c/(1+a)=500
If your not sure about his initial value of c/(1+a) then replace x with 0 in the function N:
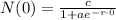
Simplify:
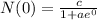

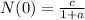
Anyways we are given:
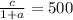 .
.
Cross multiplying gives you
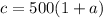 .
.
We are also giving that N(1)=1000 so plug this in:
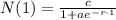
Simplify:

So this means
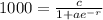
Cross multiplying gives you

We are giving that c=50000 so we have these two equations to solve:

and
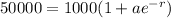
I'm going to solve
 first because there is only one constant variable here,
first because there is only one constant variable here,
 .
.

Divide both sides by 500:
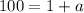
Subtract 1 on both sides:
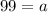
Now since we have
 we can find
we can find
 in the second equation:
in the second equation:
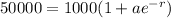 with
with
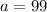
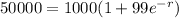
Divide both sides by 1000
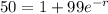
Subtract 1 on both sides:
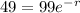
Divide both sides by 99:
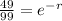
Take natural log of both sides:
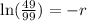
Multiply both sides by -1:
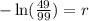
So the function N with all the write values plugged into the constant variables is: