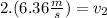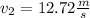Question

The first car has twice the mass of a second car, but only half as much kinetic energy. When both cars increase their speed by 9.0 m/s, they then have the same kinetic energy. What were the original speeds of the two cars? Express your answers using two significant figures separated by a comma?

Answer 1

The original speeds of the two cars were :

`6.36(m)/(s),12.72(m)/(s)`

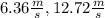
Step-by-step explanation:

Let's start reading the question and making our equations in order to find the speeds.

The first equation is :

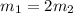`m_(1)=2m_(2)` (I)

The kinectic energy can be calculated using the following equation :

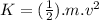`K=((1)/(2)).m.v^(2)` (II)

Where ''K'' is the kinetic energy

Where ''m'' is the mass and where ''v'' is the speed.

By reading the exercise we find that :

`K_(1)=(K_(2))/(2)` (III)

If we use (II) in (III) :

`((1)/(2)).m_(1).v_(1)^(2)=((1)/(2)).m_(2).v_(2)^(2).((1)/(2))`

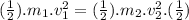
`m_(1).v_(1)^(2)=(m_(2).v_(2)^(2))/(2)` (IV)

If we replace (I) in (IV) ⇒

`2.m_(2).v_(1)^(2)=(m_(2).v_(2)^(2))/(2)`

`4.v_(1)^(2)=v_(2)^(2)`

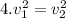
`2.v_(1)=v_(2)` (V)

'' When both cars increase their speed by
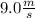`9.0(m)/(s)`, they then have the same kinetic energy ''

The last equation is :

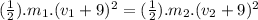`((1)/(2)).m_(1).(v_(1)+9)^(2)=((1)/(2)).m_(2).(v_(2)+9)^(2)` (VI)

If we use (I) in (VI) ⇒

`2.m_(2).(v_(1)+9)^(2)=m_(2).(v_(2)+9)^(2)`

`2.(v_(1)+9)^(2)=(v_(2)+9)^(2)`

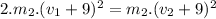
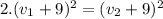
If we use (V) in this last expression ⇒

`2.(v_(1)+9)^(2)=(2.v_(1)+9)^(2)`

`2.(v_(1)^(2)+18v_(1)+81)=4v_(1)^(2)+36v_(1)+81`

`2v_(1)^(2)+36v_(1)+162=4v_(1)^(2)+36v_(1)+81`

`2v_(1)^(2)=81`

`v_(1)^(2)=40.5`

`v_(1)=√(40.5)=6.36`

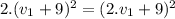
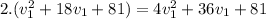
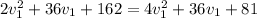
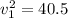
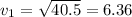
We find that the original speed
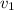`v_(1)` is
`6.36(m)/(s)`

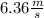
If we replace this value in the equation (V) ⇒

`2.(6.36(m)/(s))=v_(2)`

`v_(2)=12.72(m)/(s)`