Answer:
a)
 fraction of carbon−14 in a piece of charcoal remains after 14.0 years.
fraction of carbon−14 in a piece of charcoal remains after 14.0 years.
b)
 fraction of carbon−14 in a piece of charcoal remains after
fraction of carbon−14 in a piece of charcoal remains after

c)
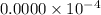 fraction of carbon−14 in a piece of charcoal remains after
fraction of carbon−14 in a piece of charcoal remains after
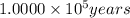 .
.
Step-by-step explanation:
The fraction of a radioactive isotope remaining at time t is given by:
![[A]=\frac{((1)/(2))^t}{t_{(1)/(2)}}](https://img.qammunity.org/2020/formulas/chemistry/college/v463ptw7nr8qsev6agvdhwkf7zogh7c7gc.png)
Taking log both sides:
![\log [A]=t\log[(1)/(2)]-\log [t_{(1)/(2)}]](https://img.qammunity.org/2020/formulas/chemistry/college/s4ft8pv19tod7ettawmtcwr9064z12sjnd.png)
[A] = fraction at given time t
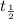 = half life of the carbon−14 =5,730 years
= half life of the carbon−14 =5,730 years
a)When , t = 14 years
![\log [A]=t\log[(1)/(2)]-\log [t_{(1)/(2)}]](https://img.qammunity.org/2020/formulas/chemistry/college/s4ft8pv19tod7ettawmtcwr9064z12sjnd.png)
![\log [A]= 14 years* (-3010)-\log [5,730 years]](https://img.qammunity.org/2020/formulas/chemistry/college/1jbtega0p71tif1y93z11nm79xplro1alr.png)
![[A]=1.065* 10^(-8)](https://img.qammunity.org/2020/formulas/chemistry/college/6cckmef1kyl90lio11st7ytli7vdqvtlie.png)
b)When , t =

![\log [A]=t\log[(1)/(2)]-\log [t_{(1)/(2)}]](https://img.qammunity.org/2020/formulas/chemistry/college/s4ft8pv19tod7ettawmtcwr9064z12sjnd.png)
![\log [A]= 1.900* 10^4 years* (-3010)-\log [5,730 years]](https://img.qammunity.org/2020/formulas/chemistry/college/y0zlkzadun7gpb2ch4jvbo7gfppfs4y2z3.png)
![[A]=0.000* 10^(-3) [/tex](https://img.qammunity.org/2020/formulas/chemistry/college/7stwd7p7eqp89k2vfcfdr3ezl7jk0mcq8q.png)
c)When , t =
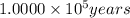
![\log [A]=t\log[(1)/(2)]-\log [t_{(1)/(2)}]](https://img.qammunity.org/2020/formulas/chemistry/college/s4ft8pv19tod7ettawmtcwr9064z12sjnd.png)
![\log [A]= 1.0000* 10^5 years* (-3010)-\log [5,730 years]](https://img.qammunity.org/2020/formulas/chemistry/college/5fw0b2zclt0p5xa51625abzichnpuhr2jg.png)
![[A]=0.0000* 10^(-4)](https://img.qammunity.org/2020/formulas/chemistry/college/6vlyiluccn5zqx0jxpm3kkeogxsnphi6be.png)