Answer:

Coefficient of
 in
in
 is 15120
is 15120
Explanation:
We know that
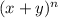 ) can be expanded in (n+1) terms by using binomial theorem and each term is given as
) can be expanded in (n+1) terms by using binomial theorem and each term is given as
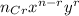
Here value of r is taken from n to 0
we have to determine the coefficient of
 in
in

in this problem we have given n=7
We have to determine the coefficient of

it means in the expansion we have to find the the 3rd power of x and therefore
r=n-3
here n=7
therefore, r=7-3=4
Hence the coefficient of
 can be determine by using formula
can be determine by using formula
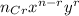
here n=7, r=4
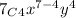
=
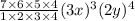
=
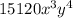
Therefore the coefficient of
 in
in
 is 15120
is 15120