Question

Questions (no partial grades if you don't show your work) 1. In a group of 6 boys and 4 girls, four children are to be selected. In how many diffeest weys ces they be selected if at least one boy must be there

Answer 1

Total number of ways will be 209

Explanation:

There are 6 boys and 4 girls in a group and 4 children are to be selected.

We have to find the number of ways that 4 children can be selected if at least one boy must be in the group of 4.

So the groups can be arranged as

(1 Boy + 3 girls), (2 Boy + 2 girls), (3 Boys + 1 girl), (4 boys)

Now we will find the combinations in which these arrangements can be done.

1 Boy and 3 girls =
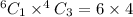`^(6)C_(1)*^(4)C_(3)=6*4`=24

2 Boy and 2 girls=
`^(6)C_(2)*^(4)C_(2)=(6!)/(4!*2!)*(4!)/(2!*2!)=15*6=90`

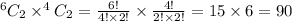
3 Boys and 1 girl =
`^(6)C_(3)*^(4)C_(1)=(6!)/(4!*2!)*(4!)/(3!)=(6*5*4)/(3 *2) *4=80`

4 Boys =
`^(6)C_(4)=(6!)/(4!*2!) =(6* 5)/(2*1)=15`

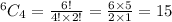
Now total number of ways = 24 + 90 + 80 + 15 = 209