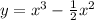Question

Solve the following initial-value problem, showing all work, including a clear general solution as well as the particular solution requested (Label the Gen. Sol. and Particular Sol.). Write both solutions in EXPLICIT FORM (solved for y). x dy/dx = x^3 + 2y subject to: y(2) = 6

Answer 1

General Solution is
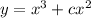`y=x^(3)+cx^(2)` and the particular solution is
`y=x^(3)-(1)/(2)x^(2)`

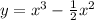
Explanation:

`x\frac{\mathrm{dy} }{\mathrm{d} x}=x^(3)+3y\\\\Rearranging \\\\x\frac{\mathrm{dy} }{\mathrm{d} x}-3y=x^(3)\\\\\frac{\mathrm{d} y}{\mathrm{d} x}-(3y)/(x)=x^(2)`

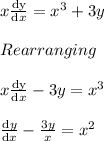
This is a linear diffrential equation of type

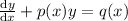`\frac{\mathrm{d} y}{\mathrm{d} x}+p(x)y=q(x)`..................(i)

here
`p(x)=(-2)/(x)`

`q(x)=x^(2)`

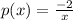
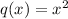
The solution of equation i is given by

`y* e^(\int p(x)dx)=\int  e^(\int p(x)dx)* q(x)dx`

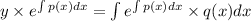
we have
`e^(\int p(x)dx)=e^{\int (-2)/(x)dx}\\\\e^{\int (-2)/(x)dx}=e^(-2ln(x))\\\\=e^{ln(x^(-2))}\\\\=(1)/(x^(2) ) \\\\\because e^(ln(f(x)))=f(x)]\\\\Thus\\\\e^(\int p(x)dx)=(1)/(x^(2))`

Thus the solution becomes

`\tfrac{y}{x^(2)}=\int (1)/(x^(2))* x^(2)dx\\\\\tfrac{y}{x^(2)}=\int 1dx\\\\\tfrac{y}{x^(2)}=x+c`
`y=x^(3)+cx^{2`

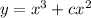
This is the general solution now to find the particular solution we put value of x=2 for which y=6

we have
`6=8+4c`

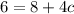
Thus solving for c we get c = -1/2

Thus particular solution becomes

`y=x^(3)-(1)/(2)x^(2)`