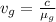Answer:
Part a)
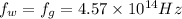
Part b)
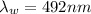
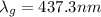
Part c)
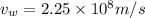
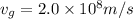
Step-by-step explanation:
Part a)
frequency of light will not change with change in medium but it will depend on the source only
so here frequency of light will remain same in both water and glass and it will be same as that in air
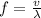
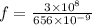
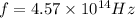
Part b)
As we know that the refractive index of water is given as

so the wavelength in the water medium is given as
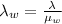

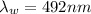
Similarly the refractive index of glass is given as
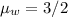
so the wavelength in the glass medium is given as


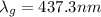
Part c)
Speed of the wave in water is given as
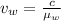
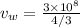
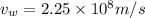
Speed of the wave in glass is given as