Question

Sam promises to pay Sandy $2,000 in four years and another $3,000 four years later for a loan of $2,000 from Sandy today. What is the interest rate that Sandy is getting? Assume interest is compounded monthly. A. 14.75% B. 16.72% C. 15.10% D. 18.08%

Answer 1

the interest rate that Sandy is getting is (C.) 15.10%

Step-by-step explanation:

Given data

in 4 year cash pay (p1) = $2000

in 8 year cash pay (p2) = $3000

time period (t1) = 4 years

time period (t2) = 8 years

loan value = $2000

To find out

interest rate

solution

first we know amount will be paid in first 4 year is

$2000
`(1+r/100)^(12t)`

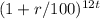
$2000
`(1+r/100)^(48)` ...................1

now we calculate the next payment will paid after 4 year i.e.

$2000
`(1+r/100)^(12t)` - $2000

$2000
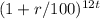`(1+r/100)^(48)` - $2000 ..................2

after full time period of payment total amount will be paid by equation 1 and 2 i.e.

$3000 = $2000
`(1+r/100)^(48)` ×$2000
`(1+r/100)^(48)` - $2000

$3000 = $2000 (
`(1+r/100)^(48)` ×
`(1+r/100)^(48)` - 1 ) .....3

now we have solve
`(1+r/100)^(48)` this eqution

so we consider
`(1+r/100)^(48)` = A

so new equation will be by equation 3

$3000/$2000 = ( A - 1 ) × A

3/2 = A² - A

solve this equation we get 2A² - 2 A - 3 = 0 so A = 1.823

now we compute A again in
`(1+r/100)^(48)` = A

`(1+r/100)^(48)` = 1.823

so rate (r) = 1.258 % / month

and rate yearly = 1.258 ×12

the interest rate that Sandy is getting yearly 15.10 %