Question

Consider this square pyramid. Recall the volume can be found using the formula V = 1/3Bh.

What is the volume of the pyramid after dilating by a scale factor of 1/4? Describe the effects.

A.) 16 m³. The volume of the new pyramid is the volume of the original pyramid times 1/64.

B.) 64 m³. The volume of the new pyramid is the volume of the original pyramid times 1/16.

C.) 256 m³. The volume of the new pyramid is the volume of the original pyramid times 1/4.

D.) 1,024 m³. The volume of the new pyramid is equal to the volume of the original pyramid.

Answer 1

The answer is A

Explanation:

Answer 2

Option A.) 16 m³. The volume of the new pyramid is the volume of the original pyramid times 1/64.

Explanation:

step 1

Find the volume of the original pyramid

The volume of the pyramid is equal to

`V=(1)/(3)Bh`

where

B is the area of the base

h is the height of the pyramid

we have

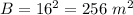`B=16^(2)=256\ m^(2)` ----> is the area of a square

`h=12\ m`

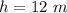
substitute

`V=(1)/(3)(256)(12)`

`V=1,024\ m^(3)`

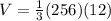
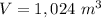
step 2

Find the volume of the new pyramid

we know that

If two figures are similar, then the ratio of its volumes is equal to the scale factor elevated to the cube

so

Let

z -------> the scale factor

x ------> the volume of the new pyramid

y -----> the volume of the original pyramid

`z^(3)=(x)/(y)`

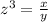
we have

`z=(1)/(4)`

`y=1,024\ m^(3)`

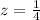
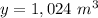
substitute and solve for x

`((1)/(4))^(3)=(x)/(1,024)`

`x=(1,024)(1)/(64)=16\ m^(3)`

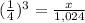
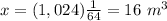
therefore

The volume of the new pyramid is the volume of the original pyramid times 1/64