Question

Solve the following congruence equations for X a) 8x = 1(mod 13) b) 8x = 4(mod 13) c) 99x = 5(mod 13)

Answer 1

a) x = 5 mod 13.

b) x = 7 mod 13.

Explanation:

a) 8x = 1 mod 13

x = 2, 16 = 3 mod 13

x = 3, 24 = 11 mod 13

x = 4, 32 = 6 mod 13

x = 5 , 40 = 1 mod 13

8x = 40

x = 5 mod 13.

b) 8x = 4 mod 13

x = 7, 56 = 4 mod 13.

7 = 4 mod 13

x = 7 mod 13.

Answer 2

a) 5+13k where k is integer

b) 20+13k where k is integer

c)12+13k where k is integer

Explanation:

(a)

`8x \equiv 1 (mod 13) \text{ means } 8x-1=13k`.

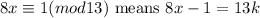8x-1=13k

Subtract 13k on both sides:

8x-13k-1=0

Add 1 on both sides:

8x-13k=1

I'm going to use Euclidean Algorithm.

13=8(1)+5

8=5(1)+3

5=3(1)+2

3=2(1)+1

Now backwards through the equations:

3-2=1

3-(5-3)=1

3-5+3=1

(8-5)-5+(8-5)=1

2(8)-3(5)=1

2(8)-3(13-8)=1

5(8)-3(13)=1

So compare this to:

8x-13k=1

We see that x is 5 while k is 3.

Anyways 5 is a solution or 5+13k is a solution where k is an integer.

b)

`8x \equiv 4 (mod 13)`

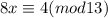
8x-4=13k

Subtract 13k on both sides:

8x-13k-4=0

Add 4 on both sides:

8x-13k=4

We got this from above:

5(8)-3(13)=1

If we multiply both sides by 4 we get:

8(20)-13(12)=4

So x=20 and 20+13k is also a solution where k is an integer.

c)

[tex]99x \equiv 5 (mod 13)[/tex

99x-5=13k

Subtract 13k on both sides:

99x-13k-5=0

Add 5 on both sides:

99x-13k=5

Using Euclidean Algorithm:

99=13(7)+8

13=8(1)+5

Go back through the equations:

13-8=5

13-(99-13(7))=5

8(13)-99=5

99(-1)+8(13)=5

Compare this to 99x-13k=5 and see that x=-1 or -1+13=12 or 12+13k is a solution where k is an integer.