Question

Prove that if a is equivalent to 5 mod (8) and b is equivalent to 3 mod (8), then 8 divides ab+1

Answer 1

See below.

Explanation:

If a = 5 mod 8 and b = 3 mod 8

then ab = 5*3 mod 8 = 15 mod 8 = 7 mod 8.

ab + 1 = 8 mod 8 = 0 mod 8 so it is divisible by 8.

Answer 2

Explanation contains the proof.

Explanation:

`a \equiv 5 (mod 8) \text{ means there is integer } k \text{ such that } a-5=8k`.

`b \eqiv 3 (mod 8) \text{ means there is integer } m \text{ such that } b-3=8m`.

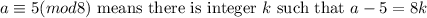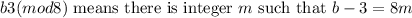We want to show that
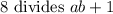`8 \text{ divides } ab+1`. So we are asked to show that there exist integer

So what is
`ab`?

`a-5=8k \text{ gives us } a=8k+5`.

`b-5=8m \text{ gives us } b=8m+5`.

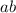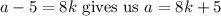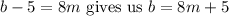So back to
`ab`....

`ab`

`=(8k+5)(8m+5)`

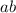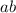
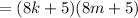
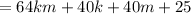`=64km+40k+40m+25` (I use foil to get this)

Factoring out 8 gives us:

`=8(8km+5k+5m)+25`

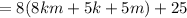
Now I could have factored some 8's out of 25. There are actually three 8's in 25 with a remainder of 1.

`=8(8km+5k+5m+3)+1`

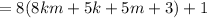
We have shown that there is integer
`n \text{ such that } ab=8n-1`.

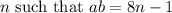The integer I found that is n is 8km+5k+5m+3.

Therefore
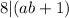`8|(ab+1)`.

//