Answer:
0.3659
Step-by-step explanation:
The power (p) is given as:
P = AeσT⁴
where,
A =Area
e = transmittivity
σ = Stefan-boltzmann constant
T = Temperature
since both the bulbs radiate same power
P₁ = P₂
Where, 1 denotes the bulb 1
2 denotes the bulb 2
thus,
A₁e₁σT₁⁴ = A₂e₂σT₂⁴
Now e₁=e₂
⇒A₁T₁⁴ = A₂T₂⁴
or
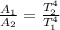
substituting the values in the above question we get
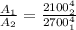
or
 =0.3659
=0.3659