Question

Problem 3.2.14a

Show that 2^2x+1 +1 is divisible by 3.

Answer 1

The given expression is divisible by 3 for all natural values of x.

Explanation:

The given expression is

`2^(2x+1)+1`

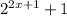
For x=1,

`2^(2(1)+1)+1=2^(3)+18+1=9`

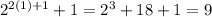
9 is divisible by 3. So, the given statement is true for x=1.

Assumed that the given statement is true for n=k.

`2^(2k+1)+1`

This expression is divisible by 3. So,

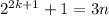`2^(2k+1)+1=3n` .... (1)

For x=k+1

`2^(2(k+1)+1)+1`

`2^(2k+2+1)+1`

`2^((2k+1)+2)+1`

`2^(2k+1)2^2+1`

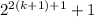
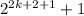
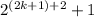
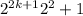
Using equation (1), we get

`(3n-1)2^2+1`

`(3n)2^2-2^2+1`

`(3n)2^2-4+1`

`(3n)4-3`

`3(4n-1)`

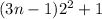
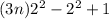
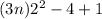
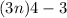
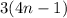
This expression is also divisible by 3.

Therefore the given expression is divisible by 3 for all natural values of x.