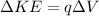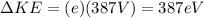Answer:
b.
Step-by-step explanation:
As we know that the electric field due to infinite line charge is given as

here we can find potential difference between two points using the relation
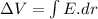
now we have
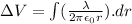
now we have
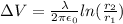
now plug in all values in it


now we know by energy conservation