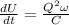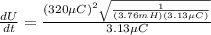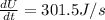Answer:
Part a)
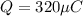
Part b)
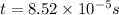
Part c)
Rate of energy = 301.5 J/s
Step-by-step explanation:
Part a)
Since energy is always conserved in LC oscillating system
So here for maximum charge stored in the capacitor is equal to the magnetic field energy stored in inductor
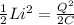
now we have
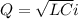
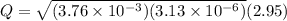
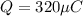
Part b)
Energy stored in the capacitor is given as

now rate of energy stored is given as
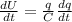
so here we also know that
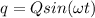
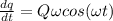
now from above equation
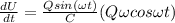
so maximum rate of energy will be given when

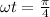

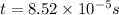
Part c)
Greatest rate of energy is given as