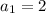Answer:
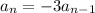 where
where
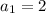
Explanation:
Recursive means you want to define a sequence in terms of other terms of your sequence.
The common ratio is what term divided by previous term equals.
The common ratio here is -6/2=18/-6=-54/18=-3.
Or in terms of the nth and previous term we could say:
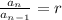
where r is -3
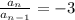
Multiply both sides by the a_(n-1).
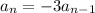 where
where