Question

a circular garden with a radius of 8 feet is surrounded by a circular path with a width of 3 feet. what is the approximate area of the path alone? use 3.14 for tt

Answer 1

178.98 square feet

Explanation:

Alright so we need to find two areas here and find the difference to find the area of the path.

The two shapes involved is a smaller circle inside a bigger circle.

Let's look at the smaller circle, the gardening area.

You are given is has a radius of 8 ft.

The area of a circle is
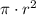`\pi \cdot r^2` where r is the radius.

So the area of the smaller circle is
`\pi \cdot 8^2`.

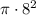Now time to look at the bigger area (which will have some overlapping area with the smaller one which will subtract out to find the area of path).

The diameter of the smaller circle was (8+8)=16 feet.

What is the diameter of the bigger one. The path is 3 ft wide so we have to add a 3 before the diameter of the smaller circle to another 3 after that diameter to get the diameter of the bigger circle. So the diameter of the bigger circle is (3+16+3)=22 feet. The radius is half the diameter so the radius is 22/2=11.

The area of the bigger circle is
`\pi \cdot 11^2`.

The area of the path=

the area of bigger circle - the area of smaller circle=

`\pi \cdot 11^2-\pi \cdot 8^2`

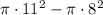
Type this into your calculator with 3.14 instead of the
`\pi` button.

178.98 square feet

Answer 2

Hello!

The answer is:

`PathArea=178.98ft^(2)`

Why?

To calculate the are of the path alone, we need to add the width of the path to the radius of the garden in order to know is radius, then, calculate the total area (using garden radius plus path width) and then, subtract it the area of the circular garden.

We know that the radius of the circular garden is equal to 8 feet, and the circular path has a width of 3 feet, so, the radius of the circular path will be:

`CPath_(radius)=8feet+Path_(width)\\\\Path_(radius)=8feet+3feet=11`

Now, calculating the areas, we have:

Garden Area:

`CircularGardenArea=\pi *radius^(2)\\\\CircularGardenRadius=\pi *8ft^(2)=3.14*64ft^(2)=200.96ft^(2)`

Total Area:

`TotalArea=\pi *(8feet+3feet)^(2)=\pi *(11ft)^(2)=3.14*121ft^(2)=379.94ft^(2)`

Now, calculating the area of the path, we have:

`TotalArea=CircularGardenArea+PathArea\\\\PathArea=TotalArea-CircularGardenArea\\\\PathArea=379.94ft^(2)-200.96ft^(2)=178.98ft^(2)`

Hence, we have that:

`PathArea=178.98ft^(2)`

Have a nice day!