Question

Can someone please explain why the answers for question 1 and 2 are different than the answers for 3 and 4

Answer 1

1) Parabola is opened up with no x-intercepts so the graph is fully above the x-axis which means all the y-coordinates in our points are positive so that is why the solution is all real numbers because it asked you to solve y>0 for x.

2) Parabola is opened up with no x-intercepts so the graph is fully above the x-axis which means all the y-coordinates in our points are positive so that is why the solution is all real numbers because it asked you to solve y>=0 for x.

3) Parabola is opened up with no x-intercepts so the graph is fully above the x-axis which means all the y-coordinates in our points are positive so that is why the solution is none because we are looking for when y<0 for x. (y<0 means y is negative)

4) Parabola is opened up with no x-intercepts so the graph is fully above the x-axis which means all the y-coordinates in our points are positive so that is why the solution is none because we are looking for when y<=0 for x. (y<=0 means negative or 0)

Explanation:

`y=ax^2+bx+c[/tex forms a parabola when graph assuming [tex]a \\eq`.

If
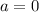`a=0`, we would have a parabola.

Anyways here are few things that might help when solving these:

1) Write ax^2+bx+c in factored form; it can lead to the x-intercepts quickly once you have it

2) The discriminant b^2-4ac:

A) It tells you if you have two x-intercepts if b^2-4ac is positive

B) It tells you if you have one x-intercept if b^2-4ac is zero

C) It tells you if you have zero x-intercepts if b^2-4ac negative

3) If a>0, then the parabola opens up.

If a<0, then the parabola opens down.

4) You might choose to test before and after the x-intercepts too, using numbers between or before and after.

Let's look at questions labeled (1)-(4).

(1) x^2-x+2>0

a=1

b=-1

c=2

I'm going to use the discriminant to see how many x-intercepts I have:

b^2-4ac

(-1)^2-4(1)(2)

1-8

-7

Since -7 is negative, then we have no x-intercepts.

The parabola is also opened up.

So if we have no-x-intercepts and the parabola is opened up (a is positive), then the parabola is above the x-axis.

So the y values for x^2-x+2 where y=x^2-x+2 is positive for all real numbers.

The solution to x^2-x+2>0 is therefore all real numbers.

(2) x^2+5x+7>=0

a=1

b=5

c=7

b^2-4ac

(5)^2-4(1)(7)

25-28

-3

Since -3 is negative, we have no x-intercepts.

The parabola is also opened up because a=1 is positive.

So again x^2+5x+7>=0 has solutions all real numbers.

(3) x^2-4x+5<0

a=1

b=-4

c=5

b^2-4ac

(-4)^2-4(1)(5)

16-20

-4

Since -4 is negative, we have no x-intercepts.

The parabola is opened up because a=1 is positive.

All the y-coordinates for our points are positive.

So y=x^2-4x+5<0 has no solutions because there are no y's less than 0.

(4) x^2+6x+10<=0

a=1

b=6

c=10

b^2-4ac

6^2-4(1)(10)

36-40

-4

Since -4 is negative, the parabola has no x-intercepts.

The parabola is opened up because a=1 is positive.

All the y-coordinates on our parabola are positive.

So y=x^2+6x+10<=0 has no solutions because there are no y's less than 0 or equal to 0.