Answer:
Rounded to nearest hundredths is 8.75.
Rounded to nearest tenths is 8.7.
Explanation:
Law of sines:

Measure of angle
 is 28 and the side opposite to it is
is 28 and the side opposite to it is
 .
.
Measure of angle
 is 105 and the side opposite to it is 18.
is 105 and the side opposite to it is 18.
Plug in to the formula giving:
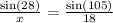
Cross multiply:
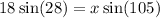
Divide both sides by sin(105):
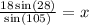 is the exact answer.
is the exact answer.
I'm going to type it in my calculator now:
18*sin(28) / sin(105) is what is going in there.
The output is 8.748589074.
Rounded to nearest hundredths is 8.75.
Rounded to nearest tenths is 8.7.