Question

Is recursion ever required to solve a problem? What other approach can you use to solve a problem that is repetitive in nature?

Answer 1

No you can not tell that recursion is ever required to solve a problem.

Recursion is required when in the problem, the solution of the input depends on the solution of the subsets of the input.

Iteration is also another form of repetitive approach we follow to solve that kind of problems.

But the difference between recursion and iteration is :

• In recursion we call the function repeatedly to return the result to next level.
• In iteration certain bunch of instructions in a loop are executed until certain conditions met.

Step-by-step explanation:

For example in the Fibonacci sequence problem, to find
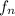`f_(n)`, we need to compute
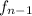`f_(n-1)` and
`f_(n-2)` before that.

• In case of recursion we just call the method Fibonacci(n) repeatedly only changing the parameter Fibonacci(n-1), that calculates the value and return it.

Fibonacci(n)

1. if(n==0 or n==1)

2. return 1.

3.else

4. return( Fibonacci(n-1)+Fibonacci(n-1) )

• But in case of iteration we run a loop for i=2 to n, within which we add the value of current
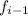  `f_(i-1)` and
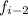  `f_(i-2)` to find the value of
  `f_(i)`

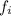
Fibonacci(n)

1. if(n<=2)

2. result = 1

3. else

4. result1 =1 and result2=1.

5. { result = result1 +result2.

6. result1= result2.

7. result2 = result.

8. }

9. output result.