Question

In a 100 mm diameter horizontal pipe, a venturimeter of 0.5 contraction ratio has been fitted. The head of water on the meter when there is no flow is 3 m (gauge). Find the rate of flow for which the throat pressure will be 2m of water absolute. Discharge coefficient for the meter is 0.97.

Answer 1

the rate of flow = 29.28 ×10⁻³ m³/s or 0.029 m³/s

Step-by-step explanation:

Given:

Diameter of the pipe = 100mm = 0.1m

Contraction ratio = 0.5

thus, diameter at the throat of venturimeter = 0.5×0.1m = 0.05m

The formula for discharge through a venturimeter is given as:

`Q=C_d(A_1A_2)/(√(A_1^2-A_2^2))√(2gh)`

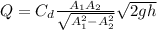
Where,

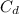`C_d` is the coefficient of discharge = 0.97 (given)

A₁ = Area of the pipe

A₁ =
`(\pi)/(4)0.1^2 = 7.85* 10^(-3)m^2`

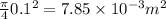
A₂ = Area at the throat

A₂ =
`(\pi)/(4)0.05^2 = 1.96* 10^(-3)m^2`

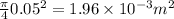
g = acceleration due to gravity = 9.8m/s²

Now,

The gauge pressure at throat = Absolute pressure - The atmospheric pressure

⇒The gauge pressure at throat = 2 - 10.3 = -8.3 m (Atmosphric pressure = 10.3 m of water)

Thus, the pressure difference at the throat and the pipe = 3- (-8.3) = 11.3m

Substituting the values in the discharge formula we get

`Q=0.97\frac{7.85* 10^(-3)* 1.96* 10^(-3)}{\sqrt{7.85* 10^(-3)^2-1.96* 10^(-3)^2}}√(2* 9.8* 11.3)`

or

`Q=(0.97*15.42* 10^(-6)* 14.88)/(7.605* 10^(-3))`

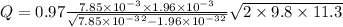
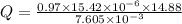
or

Q = 29.28 ×10⁻³ m³/s

Hence, the rate of flow = 29.28 ×10⁻³ m³/s or 0.029 m³/s