How many ways can a committee of five be chosen from 120 employees to interview prospective applicants.

Question

asked Sep 19, 2020 71.2k views

1 Answer

Dizzwave · Answer 1 · 2020-09-24T16:40:22+0000

Answer:

190578024 ways.

Explanation:

We are asked to find the number of ways in which a committee of 5 be chosen from 120 employees to interview prospective applicants.

We will use combinations to solve our given problem.

$_(r)^(n)\textrm{C}=(n!)/((n-r)!r!)$ , where,

n = Total number of items,

r = Number of items being chosen at a time.

Upon substituting our given values in above formula, we will get:

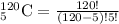
$_(5)^(120)\textrm{C}=(120!)/((120-5)!5!)$

$_(5)^(120)\textrm{C}=(120!)/(115!*5!)$

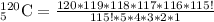
$_(5)^(120)\textrm{C}=(120*119*118*117*116*115!)/(115!*5*4*3*2*1)$

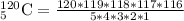
$_(5)^(120)\textrm{C}=(120*119*118*117*116)/(5*4*3*2*1)$

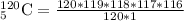
$_(5)^(120)\textrm{C}=(120*119*118*117*116)/(120*1)$

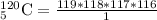
$_(5)^(120)\textrm{C}=(119*118*117*116)/(1)$

$_(5)^(120)\textrm{C}=(190578024)/(1)$

Therefore, the committee of five can be chosen from 120 employees in 190578024 ways.