Question

House Loan. Suppose you take out a home mortgage for $180,000 at a monthly interest rate of 0.5%. If you make payments of $1000/month, after how many months will the loan balance be zero?

Answer 1

It will be after 462 months

Step-by-step explanation:

We use the annuity formula for present value

`C * (1-(1+r)^(-time) )/(rate) = PV\\`

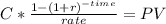
We post our know values and start solving for time:

`1000 * (1-(1+0.005)^(-time) )/(0.005) = 180,000`

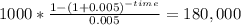
First we clear the dividend:

`1-(1+0.005)^(-time) = 180,000/1000* 0.005`

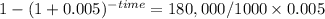
Then we clear for the power

`(1.005)^(-time) = 1-0.9`

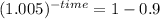
We set up the formula using logarithmic

`log_(1.005)\: 0.1 = -time`

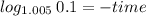
And use logarithmic properties to solve for time:

`(log\:0.1)/(log\:1.005) = -time`

`-461.6673541 = -time`

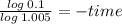
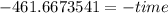
time 462 months