Answer:
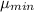 =
=

 =
=
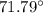
Explanation:
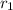 =7 in,
=7 in,
 =3 in,
=3 in,
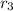 =9in
=9in
,
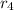 =8 in
=8 in
Transmission angle (μ ):
It is the acute angle between coupler and the output (follower) link.
Here we consider link
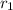 as fixed link ,
as fixed link ,
 as input link ,link
as input link ,link
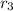 as coupler and link
as coupler and link
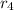 as output link.
as output link.
As we know that
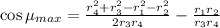
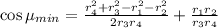
When link
 will be horizontal in left side direction then transmission angle will be minimum and when link
will be horizontal in left side direction then transmission angle will be minimum and when link
 will be horizontal in right side direction then transmission angle will be maximum.
will be horizontal in right side direction then transmission angle will be maximum.
Now by putting the values we will find
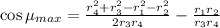
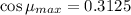

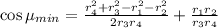
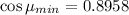
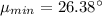
Hence, The minimum and maximum angle of transmission angle is 26.38° and 71.79° respectively.